INFORMATIQUE - Principes

INFORMATIQUE - Principes

Le traitement de l’information, au sens large, forme une part importante de l’activité humaine et elle est aussi ancienne que l’homme lui-même. L’analyse de cette activité, qui est l’objet de l’informatique, a conduit à distinguer la manipulation des connaissances, ou syntaxe, du contenu des connaissances, ou sémantique, et a permis de montrer qu’un grand nombre de démarches considérées comme «intelligentes», c’est-à-dire propres à l’homme, étaient, sinon mécaniques, du moins mécanisables.

Il devient dès lors possible d’alléger la tâche de l’homme en confiant cette partie mécanisable de l’activité intellectuelle à un dispositif automatique de traitement, c’est-à-dire à un ordinateur, de la même manière que l’on a allégé sa tâche physique par l’utilisation de machines-outils. L’ordinateur n’est donc à aucun degré un «cerveau électronique» ou une «machine intelligente», mais bien au contraire un outil sur lequel l’homme se décharge de tâches qui, justement, se sont avérées non intelligentes.

Sémantique et syntaxe

Pour communiquer entre eux, les hommes utilisent essentiellement le langage (parlé et écrit). Tout message peut être étudié sous deux aspects: celui de sa signification, c’est-à-dire des idées qu’il transmet et que l’on appelle son contenu sémantique; celui de sa structure, c’est-à-dire des règles grammaticales utilisées pour le construire et qui forment l’aspect syntaxique. Ces deux aspects sont fondamentalement distincts dans la mesure où un même message peut être rédigé en français ou en chinois, ce qui fait appel à des syntaxes différentes, tout en conservant le même sens. L’information, au sens de l’informatique, étant ce qui forme le support des connaissances, il s’ensuit que l’informatique ne s’intéresse qu’aux aspects syntaxiques, à l’exclusion des aspects sémantiques.

Par conséquent, deux messages ayant même sens et rédigés respectivement en chinois et en français sont considérés, du point de vue de l’informatique, comme deux messages totalement distincts. En simplifiant, on peut dire que, pour une langue déterminée, un dictionnaire permet de connaître la sémantique de la langue, alors que la grammaire décrit la syntaxe (règles de conjugaison, accord des participes, règles du pluriel des mots, etc.).

De façon plus générale, étant donné un ensemble d’éléments, l’informatique ne s’intéresse qu’aux règles permettant de combiner ces éléments entre eux, c’est-à-dire aux structures syntaxiques définies sur cet ensemble et aux règles opératoires permettant de passer d’une structure à une autre, en faisant systématiquement abstraction de toute sémantique.

Informatique et mathématiques

Les premiers ordinateurs ont été construits pour faire des calculs à grande vitesse et pendant très longtemps ont été désignés par le terme de «calculatrices». Ultérieurement, on s’est aperçu que les capacités de traitement de ces machines dépassaient très largement le domaine du calcul numérique et qu’elles étaient utilisables par exemple pour la gestion des entreprises, pour la traduction des langues, ou pour l’aide au diagnostic en médecine.

Cela explique que l’on soit passé historiquement de la notion de «calculatrice» à celle de «système automatique de traitement de l’information». Ce n’est cependant pas par hasard que les ordinateurs sont nés des tentatives pour automatiser les opérations de calcul; le calcul numérique, du point de vue de l’informatique, est en effet un domaine à contenu sémantique nul où l’on se contente de manipuler des symboles sans signification selon des règles préétablies, manipulation qu’une machine est capable d’effectuer. Il en va de même du calcul algébrique, où l’on manipule des variables à la place des nombres.

Si l’on considère l’ensemble des mathématiques, on constate que les objets que l’on y définit n’ont pas d’existence en dehors de leur définition et que leurs seules propriétés sont celles qui découlent de ces définitions. Dans ces conditions, faire une démonstration, c’est combiner entre elles un certain nombre de propriétés selon des règles préétablies. Ces dernières sont l’objet de la logique mathématique, qui vise à formaliser le raisonnement déductif, c’est-à-dire justement à ramener le raisonnement mathématique à une manipulation de symboles sans signification. C’est en ce sens qu’il faut interpréter la célèbre boutade du logicien Bertrand Russell selon laquelle «les mathématiques sont une science où l’on ne sait pas de quoi l’on parle ni si ce qu’on dit est vrai». La démarche des logiciens visant à ramener la totalité des mathématiques à des manipulations formelles de symboles relève typiquement de l’informatique, même si les logiciens n’en ont pas toujours été conscients, et conduit, de ce point de vue, à considérer les mathématiques comme un domaine où la totalité de la sémantique est réductible à la syntaxe, ce que Léon Brillouin énonçait sous la forme suivante: «Le contenu informationnel des mathématiques est nul.»

Automates et langages formels

Langage formel

Un langage formel est, par définition, un langage ne possédant qu’une syntaxe et pas de sémantique. Un tel langage est très différent des langages naturels puisqu’il ne comporte qu’une grammaire et que le sens des mots n’intervient pas. C’est cependant en partant, non pas de la linguistique, mais de l’activité linguistique des individus, et en cherchant à résoudre un double problème, à savoir celui de l’individu parlant – capable, en apprenant un nombre fini de mots et de phrases, de former ensuite un nombre infini de phrases syntaxiquement correctes –, et celui de l’individu écoutant – capable de reconnaître la correction syntaxique d’une phrase qu’il n’a jamais entendue au préalable –, que Noam Chomsky aboutit à la théorie des grammaires génératives et des automates de reconnaissance.

Selon Chomsky, un langage formel L est formé par un quadruplet:

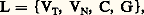oùV^T est un ensemble d’éléments non définis (les mots) appelé vocabulaire terminal,V^N un ensemble d’éléments non définis appelé vocabulaire non terminal et comportant un élément P dit axiome, C une opération interne sur V^T et sur V^N appelée concaténation (ou juxtaposition de deux éléments), qui est associative, et G une grammaire formée d’un certain nombre de règles dites règles de réécriture. Une phrase d’un langage formel sera une suite quelconque d’éléments de V^T obtenue à partir de P en appliquant les règles de G.

Choisissons par exemple un langage L¹, tel que:

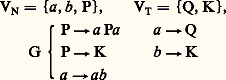(le symbolesignifie «peut se remplacer par»).

Partant de P et en utilisant la règle Pa Pa , on aboutit à a Pa ; en appliquant à nouveau la même règle au symbole de P dans a Pa , on obtient a (a Pa )a , soit aa Paa , et ainsi de suite, chaque règle pouvant être utilisée à tout moment et autant de fois que l’on veut pour aboutir à une «phrase» n’ayant que des mots du vocabulaire terminal.

Les phrases QKQ, QQKQQ, ..., et de façon plus générale les phrases Q^p KQ^p , c’est-à-dire toutes celles ayant un nombre p de mots Q, suivi du mot K, suivi du même nombre p de mots Q, seront des phrases du langage L¹. Ce même langage comprendra aussi les phrases QKKQ, QKKQK, QKKKQKK, etc.

Le mécanisme précédent résout le premier problème évoqué, à savoir celui de la génération d’un nombre infini de phrases d’un langage à partir d’un vocabulaire fini et d’un nombre fini de règles de grammaire. Le second problème, qui consiste à trouver un mécanisme permettant de reconnaître si une «phrase» quelconque appartient ou non à un langage déterminé, sera résolu par la définition d’un «automate de reconnaissance» qui est un dispositif ayant un nombre fini d’états et muni d’une mémoire finie ou infinie. Un tel «automate» sera capable de «lire» une phrase de gauche à droite et, arrivé à l’extrémité de la phrase, de «dire» si la phrase appartient ou non au langage qu’il est capable de reconnaître, étant entendu que l’automate fonctionne selon un nombre fini de règles fixes données à l’avance. Un des grands mérites de Chomsky a été de proposer une classification des langages formels selon leur degré de complexité syntaxique, c’est-à-dire selon le degré de complexité de l’automate de reconnaissance.

Langages réguliers et automates à nombre fini d’états

Les langages réguliers , définis initialement par Stephan Cole Kleene, sont ceux dont la grammaire ne comporte qu’un seul type de règles de réécriture, à savoir qu’un mot non terminal ne peut être réécrit que sous la forme d’un mot non terminal suivi d’un mot terminal, ou l’inverse, ou encore sous la forme d’un mot terminal.

Prenons par exemple le langage suivant:

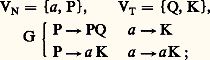on démontre aisément que ce langage se compose de toutes les phrases de la forme:

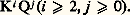Un automate à nombre fini d’états:

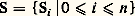possède une «tête de lecture» devant laquelle défile un ruban divisé en cellules, chacune des cellules pouvant recevoir un symbole terminal; l’automate est muni d’un nombre fini de règles du type:

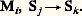Ces règles signifient que si l’automate est dans l’état S^j et que sa tête de lecture est positionnée devant une cellule contenant le symbole terminal Mⁱ , il passe alors dans l’état S^k et déplace le ruban d’une cellule vers la gauche (fig. 1).

Une phrase d’un langage étant écrite sur le ruban, à raison d’un mot par cellule, et encadrée à droite et à gauche par des cellules vides (B), on met l’automate dans l’état S⁰ en le positionnant sur le symbole le plus à gauche du ruban; l’automate change alors d’état en déplaçant le ruban d’une case vers la gauche aussi longtemps qu’il existe des règles du type Mⁱ , S^jS^k ; arrivé dans une situation Mⁱ , S^j , où il n’existe pas de règle du type précédent, l’automate est bloqué. Si, par contre, ayant lu toute la phrase, l’automate se retrouve dans la situation B, S⁰, on dit que la phrase a été reconnue.

Il est facile de voir que l’automate défini par:

reconnaît toutes les phrases de la forme Kⁱ Q^j (i 閭 1, j 閭 0), à l’exclusion de toute autre phrase.

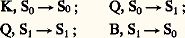De façon plus générale, on démontre que pour tout langage régulier on peut construire un automate à nombre fini d’états qui reconnaisse ce langage.

Les langages réguliers ont donc une grammaire très simple et ont la propriété commune d’être reconnaissables par un automate à nombre fini d’états, bien que les phrases du langage puissent être de longueur infinie.

Langages contexte-libres et automates à pile de mémoire

Les langages contexte-libres ou langages de Chomsky forment une classe très importante en pratique puisque la plupart des langages de programmation des ordinateurs sont, à peu de chose près, de ce type. Comme les langages réguliers, ils sont définis par un quadruplet L =V^T, V^N, C, G, mais cette fois les règles de G sont de la forme a ⁱ﨏, où a ⁱ est un symbole non terminal et 﨏 une suite quelconque de symboles pris dansV^T ouV^N. La terminologie de contexte-libre vient de ce que la règle de réécriture de a ⁱ ne dépend pas des symboles placés à gauche et à droite de a ⁱ , c’est-à-dire qu’elle ne dépend pas du contexte.

Défini par le quadruplet:

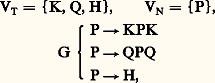ce langage est composé de toutes les phrases où la partie de la phrase qui suit H est symétrique de celle qui précède H: QKHKQ, KKQHQKK, QKKQKHKQKKQ, etc.

Les automates permettant de reconnaître les langages de Chomsky sont des automates à pile de mémoire. Ceux-ci se composent d’un automate à nombre fini d’états comportant, d’une part, une tête de lecture devant laquelle peut défiler de gauche à droite un ruban divisé en cellules et, d’autre part, une tête de lecture-écriture capable d’écrire et de lire dans les cellules d’un deuxième ruban (appelé ruban mémoire), qui est infini d’un seul côté et peut se déplacer de droite à gauche et de gauche à droite devant la tête de lecture-écriture (fig. 2).

En simplifiant quelque peu, on dira que l’on écrit une phrase sur le premier ruban à raison d’un symbole par cellule et que l’on positionne ce ruban de façon à placer la tête de lecture en face du premier symbole à gauche de la phrase; le ruban mémoire est placé de manière que la première cellule à gauche soit sous la tête de lecture-écriture et l’automate est dans l’état S⁰.

L’automate est alors muni d’un ensemble fini de règles de la forme:

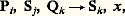où Pⁱ désigne un symbole lu sur le premier ruban, S^j l’état de l’automate et Q^k le symbole lu sur le ruban mémoire; dans ces conditions, la règle indique que l’automate passe dans l’état S^k et effectue une action qui dépend de x (si x est un mot, celui-là est écrit sur le ruban mémoire qui se déplace d’une cellule vers la gauche; si x est égal à E, on efface le mot écrit dans la cellule du ruban mémoire situé sous la tête de lecture-écriture et on déplace ce ruban d’une cellule vers la droite; si x est égal à zéro, il n’y a pas d’action sur le ruban mémoire). À l’issue de cette action, le premier ruban se déplace d’une cellule vers la gauche.

On dira que l’automate à pile a reconnu une phrase si, partant de la situation initiale, on arrive à appliquer les règles de manière à terminer dans la situation B, S⁰, B.

Pour le «langage miroir» évoqué ci-dessus, il est facile de définir un ensemble de règles qui permette de reconnaître toutes les phrases de ce langage et celles-là seulement: un premier groupe de règles permet de recopier sur le ruban mémoire tous les mots lus sur le premier ruban jusqu’à la rencontre du marqueur central H; à partir de là, un deuxième groupe de règles permet de vérifier, en faisant défiler le ruban mémoire dans l’autre sens, que la deuxième partie de la phrase est bien symétrique de la première.

De façon générale, à tout langage de Chomsky correspond un automate à pile de mémoire qui rend possible la reconnaissance de toutes les phrases de ce langage, à l’exclusion de toutes les autres.

Automates de Turing

Les automates définis dès 1936 par le mathématicien anglais Alan Mathison Turing se sont révélés d’excellents nodèles abstraits des ordinateurs réalisés à partir de 1943.

Un automate de Turing est composé d’un automate à nombre fini d’états, muni d’une tête de lecture-écriture devant laquelle se trouve un ruban divisé en cellules et qui peut se déplacer de droite à gauche et de gauche à droite. Cet automate est muni d’un nombre fini de règles qui peuvent être de trois types:

Sⁱ Q^j P^m S^k ; si l’automate est dans l’état Sⁱ et si la cellule située sous la tête de lecture-écriture contient Q^j , l’automate remplace Q^j par P^m et passe dans l’état S^k ;

Sⁱ Q^j DS^k ; dans les mêmes conditions, on déplace le ruban d’une cellule vers la droite et l’automate passe à l’état S^k ;

Sⁱ Q^j GS^k ; dans ce cas, on déplace le ruban d’un rang vers la gauche.

Turing a montré que toute fonction calculable était calculable par un automate de ce type, c’est-à-dire qu’étant donné une fonction calculable il était toujours possible de définir un ensemble de règles du type évoqué ci-dessus qui lui permette d’effectuer le calcul.

Algorithmes et décidabilité

Un algorithme est une suite finie de règles à appliquer dans un ordre déterminé à un nombre fini de données pour arriver, en un nombre fini d’étapes, à un certain résultat, et cela indépendamment des données; par exemple, l’algorithme de l’addition permet de faire l’addition de deux nombres quelconques en partant des chiffres les plus à droite et en opérant de droite à gauche. Un algorithme étant une description de la suite des opérations à faire, il est clair que la manière de le rédiger dépendra du dispositif (homme ou machine) chargé de l’exécuter et qu’un algorithme écrit en turc par exemple n’est pas un algorithme pour celui qui ignore cette langue. De ce point de vue, un programme destiné à un ordinateur est très précisément un algorithme, et un langage de programmation est un langage permettant d’écrire un algorithme qu’un ordinateur saura exécuter. De ce même point de vue, l’ensemble des règles d’un automate à pile de mémoire est un algorithme permettant de savoir si une phrase écrite sur le ruban d’entrée appartient ou non à un certain langage.

Si l’algorithme ne permet pas d’arriver au résultat en un nombre fini d’étapes, on dit que l’on a un pseudo-algorithme. Pour déceler un pseudo-algorithme, il faudrait pouvoir construire un algorithme qui, appliqué à un quelconque pseudo-algorithme, permettrait de trancher la question. Malheureusement, et ce résultat est d’une extrême importance, on démontre qu’il est impossible de construire un tel algorithme; ce problème est indécidable. En termes de programmation, cela revient à dire qu’il est impossible d’écrire un programme qui, prenant un autre programme comme donnée, permettra de savoir si ce programme fournira des résultats au bout d’un temps fini.

Le caractère indécidable de certains problèmes n’autorise aucune spéculation sur les limites de l’esprit humain ou sur la vanité de toute logique. Il s’agit là de démonstrations de caractère technique à l’intérieur d’un système de logique et elles n’ont pas plus de conséquences «philosophiques» que le théorème de Pythagore.

Encyclopédie Universelle. 2012.